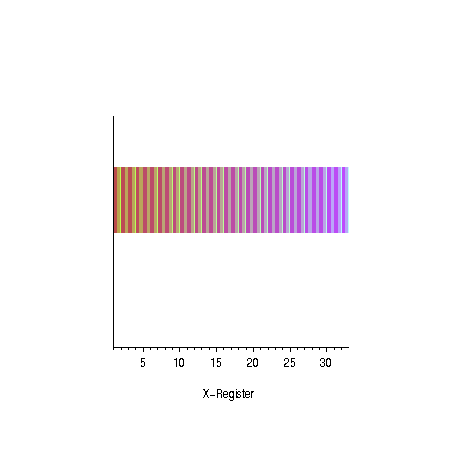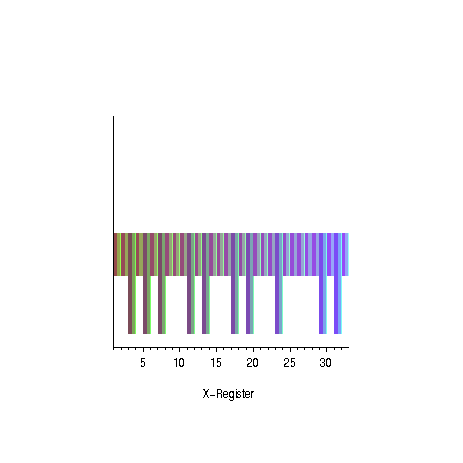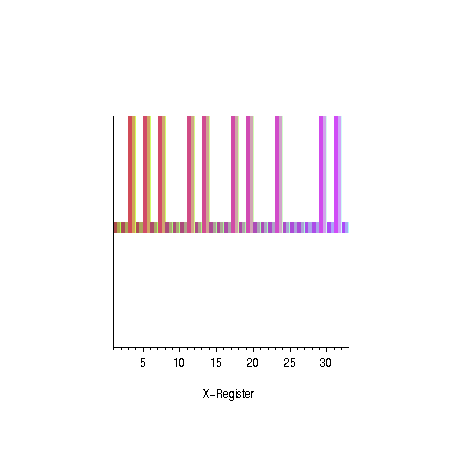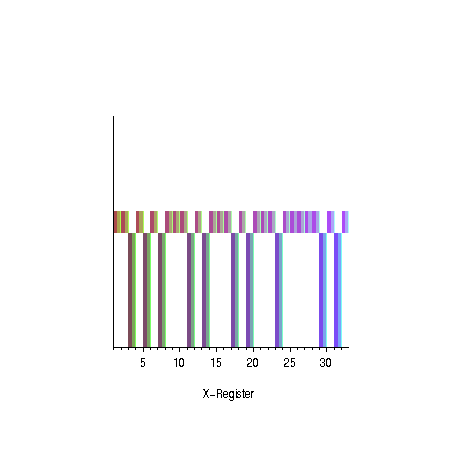Vorlesung im Wintersemester 2018/19
Quantum Computing – Grundlagen der Quanteninformationsverarbeitung
(Dr. Markus Grassl)
| Vorlesung, 2,5 SWS, ECTS-Studium, ECTS-Credits: 5 |
| Zeit: | dienstags, 08:00-10:00 Uhr
|
| Ort: | Seminarraum
Tandemlabor SR 307 |
| Prüfung: | mündlich, nach Vereinbarung,
Anmeldung zur Prüfung via E-Mail |
Quantenrechner bieten die Perspektive, zumindest bestimmte Probleme
mit einer geringeren Komplexität zu lösen als klassische
Computer. Allen voran sind als Beispiele der Algorithmus von Shor zur
Faktorisierung ganzer Zahlen in polynomialer Zeit sowie der
Algorithmus von Grover zur Urbildsuche zu nennen.
Nach einer Einführung in das auf den Prinzipien der
Quantenmechanik basierende Berechnungsmodell werden verschiedene
Quantenalgorithmen genauer betrachtet. Ergänzend werden
grundlegende Verfahren zur Implementierung von
Quantentransformationen, Fehlerkorrektur und Fehlertoleranz
besprochen. Ein weiteres Themengebiet umfasst Grundbausteine der
Quantenkryptographie.
Die Vorlesung wendet sich an Studierende der Fachrichtungen Physik,
Informatik, Mathematik sowie Elektrotechnik im letzten Jahr des
Bachelorstudiums oder im Masterstudium.
Die erforderlichen Grundlagen werden in der Vorlesung vermittelt.
Interessenten werden gebeten, per E-Mail Kontakt aufzunehmen. Sprechstunde nach Vereinbarung.
- Lecture 1
- bra-ket notation
- ket |x⟩: column vector
- bra ⟨y|: row vector
- projection P=|x⟩⟨x|
- Postulate I:
Quantum states are described by normalised states in a Hilbert space
- Postulate II:
Measurements are described by Hermitian operators A.
- Lecture 2
- Postulate III:
a) discrete-time dynamics: The change of a quantum state from
time t1 to time t2 is
diven by a unitary operator U=U(t1,t2)
b) continuous-time dynamics: In general, the dynamics of a
quantum system is described by the Schrödinger
equation.
- Postulate IV:
The Hilbert space of a composite quantum system is the tensor
product of the Hilbert spaces of its components.
- product state: A state that can be written as
|Ψ⟩ = |ψ⟩⊗|ϕ⟩.
- entangled states: All states that are not product states.
- ensemble of quantum states: The quantum system is with
probability pi in the state
|ψi⟩.
- density matrix of an ensemble:
ρ = ∑i
pi|ψi⟩⟨ψi|.
The number of quantum states in the ensemble can be
arbitrary, unrelated to the dimension d of the
Hilbert space.
- spectral decomposition:
ρ = ∑j
λj|ϕj⟩⟨ϕi|, j=1,…,r
≤ d.
- pure/mixed states:
The density matrix of a pure state |φ⟩ is ρ =
|φ⟩⟨φ|.
In the spectral decomposition, there is only one non-zero
eigenvalue λ1=1, and one has
Tr(ρ)=Tr(ρ2)=1.
A state with more than one non-zero eigenvalue is
called mixed state.
- Measuring one part of an entangled states has an effect on
the other part of the system.
Example: |Ψ+⟩ = (|00⟩ + |11⟩)/√2
- Lecture 3
- quantum bit (qubit):
two-dimensional Hilbert space, different parameterisations of
pure states
- states |ψ⟩ and eiϕ|ψ⟩ cannot be distinguished; normalisation will
often be omitted
- Pauli spin matrices σx, σy, σz
- expectation values ⟨σj⟩∈[-1,1] define a point in three-dimensional real space
⇒ qubit state is represented by Bloch vector on Bloch sphere/ball
- eigenstates of Pauli matrices
- single qubit operations
- rotations
around x-, y-, z-axis
- Any special unitary operation U ∈SU(2) is a product of three
rotations (Euler decomposition).
- Hadamard transformation H interchanges
eigenbases of σx and σz
- simple quantum algorithm: fair coin toss (true randomness)
- n-qubit system:
basis states
|x1,x2,…,xn⟩
labelled by bit strings of length n, dimension 2n
- Lecture 4 (Ulrich Seyfarth)
- One Time Pad
- generation of common key for symmetric encryption
- problems of implementation (key exchange)
- Mformation theoretically secure
- Quantum key distribution (BB84)
- requires quantum channel and authenticated classical channel
- quantum information is sent as a stream of single qubits
which are, for example, encoded into the polarization of
single photons
- Prepare & Measure scheme:
Alice chooses randomly Z- or X-basis
and sends a random eigenstate to Bob who measures in a
random basis
- measurement in the same basis gives always correct
result, but a completely random result for the wrong basis
- Alice and Bob discuss publicly using the classical
channel which bases were used
- eavesdropper might measure photons in random basis, and
then sends an accordingly prepared photon to Bob (intercept-resend attack)
- attacks are detectable due to induced errors, as unknown
quantum information cannot be copied perfectly due
to No-Cloning Theorem
- Prepare & Measure vs. entanglement based
protocol
- post-processing (error correction & privacy
amplification)
- imperfect implementation (single photon source,
detectors, quantum channel, preparation, side-channel
attacks, continuous variable vs. discrete variable)
- References
Charles H. Bennett and Gilles Brassard.
"Quantum cryptography: Public key distribution and coin tossing".
In Proceedings of IEEE International Conference on
Computers, Systems and Signal Processing, 1984.
http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf
W. K. Wootters and W. H. Zurek.
"A single quantum cannot be cloned".
Nature, vol. 299, pp. 802-803 (1982).
DOI: 10.1038/299802a0
- Lecture 5
- reversible Boolean functions
- arbitrary Boolean function f: {0,1}n → {0,1}m
- add additional output bits in order to make the function injective, if necessary
- add additional input bits to make the number of input and output bits equal
- new partial function f' with f'(x,0) = ( f(x), g(x) )
- specify the values of f' for the remaining inputs such that f' is injective
- general construction: f': {0,1}n+m → {0,1}m+m;
f'(x, y) =(x, x⊕y)
- reversible AND gate (Toffoli gate):
- f(x,y,z) = (x,y,xy⊕z)
- AND: f(x,y,0) = (x,y,xy)
- NAND: f(x,y,1) = (x,y,xy⊕1)
- quantum version: Uf :
|x⟩|y⟩ ↦ |x⟩|y⊕f(x)⟩
(on basis states)
- Uf with f(x)=x:
|x⟩|y⟩ ↦ |x⟩|x⊕y⟩
(CNOT gate)
- Hadamard transformation on n qubits
- quantum parallelism
- a single application of Uf yields a
superposition of all points (x, f(x) )
- quantum state of the function graph: ∑x |x⟩|f(x)⟩
- measuring the first register: random point of function graph
- measuring the second register: superposition of
preimages of a random value y0
∑f(x)=y0 |x⟩|y0⟩
- Lecture 6
- quantum state encoding a function graph:
probability of measuring a particular function value
- Deutsch algorithm
- Given a Booelean
function f : {0,1}→{0,1},
decide whether f is constant or not.
- classical algorithm:
- a single evaluation of the function does not provide
any information
- two function evaluations are sufficient
- quantum algorithm:
- a single application of Uf is
sufficient
- detailed analysis
- quantum circuit
- identities for X, Z, H and CNOT
David Deutsch.
"Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer".
Proceedings of the Royal Society A, vol. 400, no. 1818, pp. 97-117, July 1985.
DOI: 10.1098/rspa.1985.0070
JSTOR: www.jstor.org/stable/2397601
- Lecture 7
- Deutsch-Joza algorithm
- given: a boolean function f : {0,1}n→{0,1}
- outpute:
(A) f is not constant or
(B) f ist not balanced
- classical algorrithm: worst case 2n-1+1function evaluations,
on average over all functions: at most 3 function evaluations (see Table 1 in the paper belows)
- quantum algorithm: a single application of Uf
David Deutsch und Richard Jozsa.
"Rapid Solution of Problems by Quantum Computation".
Proceedings of the Royal Society A, vol. 493, no. 1907, pp. 553-558, Dezember 1992.
DOI: 10.1098/rspa.1992.0167
JSTOR: www.jstor.org/stable/52182
- diagonal version of Uf:
|x⟩ ↦ (-1)f(x)|x⟩
- Lecture 8
- algorithm of Bernstein & Vazirani:
- given: fa(x)=(-1)a⋅x
- find: a∈{0,1}n
- evaluating the classical function fa yields only 1 bit per evaluation
- a single application of Uf is
sufficient to obtain the vector a via n single-qubit measurements
- Simons's algorithm
- classical function fs:
{0,1}n
→{0,1}m (m≥n),
addtionally: fs(x)=fs(y)
if and only if x=y
or x=y⊕s for a fixed, but unknown vector s∈{0,1}n
- find the vector s
- classical algorithm: worst
case 2n-1+1 evaluations
of fs, to find a collision
of f or decide that there is none
birthday phenomenon: O(2n/2)
evaluations if there is a collision
D. R. Simon.
"On the power of quantum computation."
Proceedings 35th Annual Symposium on Foundations of Computer Science (FOCS 1994), pp. 116-123, November 1994.
DOI: 10.1109/SFCS.1994.365701
- Lecture 9
- Simons's algorithm (continued)
- quantum algorithm: a single application
of Uf yields a random
vector b with b·s = 0
-
repeat the quantum algorithm until n-1 linearly
independent vectors have been found;
expected running time O(n), but termination not guaranteed
- the homogeneous linear system of n-1 equations
for s has one non-trivial
solution s0
- output s=s0,
if f(0)=f(s0); otherwise
output S=0
- quantum algorithm without while-loop
- preparation of a fixed initial state
- sequence of elementary unitary quantum operations
(with a fixed number of parameters/acting on a fixed
number of subsystems)
- measurement with respect to a fixed basis
- intermediate partial measurements can be postponed to
the very end
(conditional quantum operations)
- hybrid quantum algorithm:
classical program (with while-loops) calling quantum
sub-routines with a fixed number of quantum operations
- Lecture 10
- Classical cryptography
- one-time pad
- Diffie-Hellman-Merkle key generation
- public parameters prime p and base g
- Alice and Bob choose randomly private exponents a and b
- Alice sends ga mod p to Bob;
Bob sends ga mod p to Alice
- the secret common key
is(ga)b
mod p =
(gb)a
mod p
- computational security based on hardness to
compute the discrete logarithm
dlogg (ga) = a
Whitfield Diffie, Martin E. Hellman.
"New Directions in Cryptography."
IEEE Transactions on Information Theory, vol. 22, no. 6,
pp. 644-654, 1976.
DOI: 10.1109/TIT.1976.1055638
- RSA encryption
- public key: modulus N, exponent e
- private key:
- factorisation N = pq
- inverse exponent e, i. e., de = 1 mod φ(N), gcd(e,φ(N) = de + sφ(N)
- Eulers's totient function:
φ(N) equals the number of
positive integers smaller than N
that are co-prime to N
- for different primes p and q we have
φ(N)=(p-1)(q-1)
- encryption: m → me mod N
- decryption me →
(me)d = m mod N
- attacking the private key:
factoring N = pq allows to compute
φ(N) and d = e-1
mod φ(N)
- attacking individual cipher texts:
e-th root of me
bzw. aus me + kN, with an unknown integer k
R. L. Rivest, A. Shamir, and L. Adleman.
"A Method for Obtaining Digital Signatures and Public-Key
Cryptosystems."
Communications of the ACM, vol. 21, no. 2, pp. 120-126, 1978
DOI: 10.1145/359340.359342
- Integer factorisation
- find non-trivial factors of an integer N
- classical: runtime of the best general algorithm (number field sieve);
O(exp[(C+o(1))(log N)1/3(log log N)2/3]) mit C=(64/9)1/3≈1.923
- reduction to order finding:
- find the smallest positive integer r>0 such
that ar ≡ 1 mod N
- if r is even
and ar/2≠-1 mod N, then
gcd(ar/2±1,N) yields a non-trivial
factor of N
- consider the graph of the periodic function f(x)=ax mod N
- periodic function f(x)=ax mod N
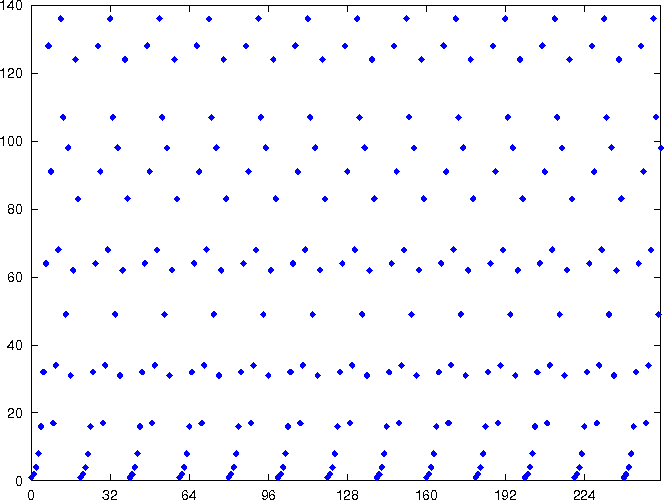 |
| graph of 2x mod 165 |
Lecture 11: Shor's Algorithms
- Integer factorisation
- reduction to order finding
- prepare the quantum state
∑x|x⟩|ax mod N⟩
- measuring the second register yields a state of the form
∑k|x0+kr⟩|ax0=y0 mod N⟩
- discrete Fourier transformation (DFT) transforms the offset x0 into a global phase factor,
and the period r into the (approximate) inverse period
- measuring the first register yields an approximation x/M of a multiple of the inverse period 1/r
- continued fraction approximation yields the
rational number c'/d' closest to x/M with
denominator d' ≤ N for M ≥ N2
- test, whether d' equals the order of a mod N
- Fourier transformation with length M=2×3×5×7×11×…
Peter W. Shor.
"Algorithms for quantum computation: discrete logarithms and factoring."
Proceedings 35th Annual Symposium on Foundations of Computer Science (FOCS 1994), pp. 124-134, November 1995.
DOI: 10.1109/SFCS.1994.365700
- Fourier transformation with length M=2m
Peter W. Shor.
"Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer."
arXiv:quant-ph/9508027
- discrete logarithm
- given: basis g and modulus p (prime)
task: find integer a with c=ga mod p
- use the function f(x,y)=cx g-y=gax-y mod p
- function graph: |ψ⟩=1/(p-1) ∑x∑
y|x⟩|y⟩|cx
g-y mod p⟩
- after measuring the third register, the state of the
first two registers corresponds to the line
y=ax+y0 with slope a and
some random offset y0
- two-dimensional discrete Fourier transformation DFT(p-1)×(p-1)=DFT(p-1)⊗DFT(p-1)
transforms the offset into a global phase and yields a
line through the origin with inverse slope
- measuring the first two registers allows to deduce the
slope a unless the result was the point (0,0)
- optimisation:
- one might use properties of N that are easy to
detect to optimise e.g. the modular exponentiation
- but do not over-simplify the problem
John A. Smolin, Graeme Smith, Alex Vargo
"Oversimplifying quantum factoring"
Nature, vol 499, pp. 163-165 (2013)
DOI: 10.1038/nature12290
arXiv:1301.7007 [quant-ph]
Lecture 12
- Quantum Fourier transformation
- recursive decomposition of Fourier transformation of
length M = 2m into Hadamard gate, diagonal
matrix T, and Fourier transformation of length M = 2m-1
- matrix T is the product of m two-qubit
controlled-phase operations
- overall complexity O(m2), compared to O(m 2m)
for classical fast Fourier transformation (FFT)
- Hidden Subgroup Problem (HSP)
- given: a (finite) group G and a
function f, that labels the cosets of an unknown
subgroup H≤G,
i. he, f(x)=f(y)
if and only if x y-1 ∈ H
- task: find generators for H
- there are efficient quantum algorithms for all (finite)
Abelian groups and some non-Abelian groups
- Simon's problem: G =(Z2)n, H={0,s}
- factoring/order finding:
G = Zφ(N), H = ⟨a⟩
- discrete logarithm
G = Zp-1 × Zp-1, H=⟨(1,a)⟩
- phase estimation
- given a unitary U and an eigenstate
|ψ⟩, find the corresponding
eigenvalue λ = eiϕ
with U|ψ⟩ = λ|ψ⟩
- idea: turn global phase into relative phase and use constructive/destructive interference
- using a controlled-U operation one maps
(|0⟩ + |1⟩) |ψ⟩
→
(|0⟩ + λ|1⟩) |ψ⟩
(phase kick-back)
- Hadamard transformation and measuring the first qubit
- quantum advantage: use n qubits in the first
register and controlled-U2m transformations
Lecture 13: Quantum Search Algorithm
- searching a pre-image x of a Boolean function
f : {0,1}n→{0,1}
with f(x)=1
- satisfiability problem for Boolean functions (3-SAT, NP-complete)
- false advertisement: not searching a classical phone book or
a classical database
Lov K. Grover.
"A fast quantum mechanical algorithm for database
search."
arXiv:quant-ph/9605043
- reduction to dynamics in a two-dimensional space
(superposition of all states with f(x)=1 or f(x)=0)
- geometric interpretation as combination of two reflections,
see Kapitel 6.3 in
Matthias Homeister.
Quantum Computing verstehen.
Heidelberg: Springer, 2013.
ISBN: 978-3-658-10455-9
Lecture 14: Quantum Search Algorithm (continued)
- exact solution of the recurrence relation for the amplitudes
Michel Boyer, Gilles Brassard, Peter Høyer and Alain Tapp.
"Tight bounds on quantum searching."
Fortschritte der Physik, vol. 46, no. 4-5, pp. 493-505,
June 1998.
DOI: 10.1002/(SICI)1521-3978(199806)46:4/5<493::AID-PROP493>3.0.CO;2-P
arXiv:quant-ph/9605034
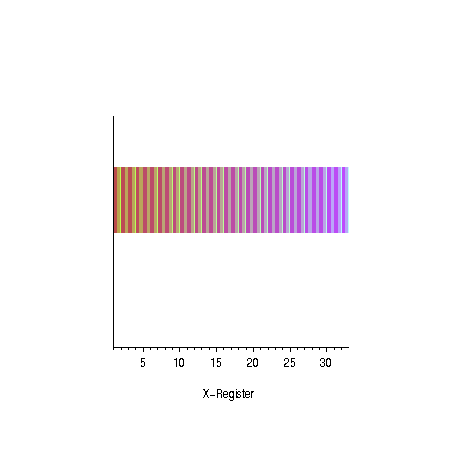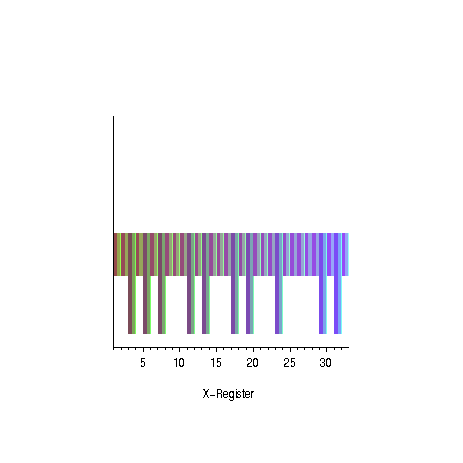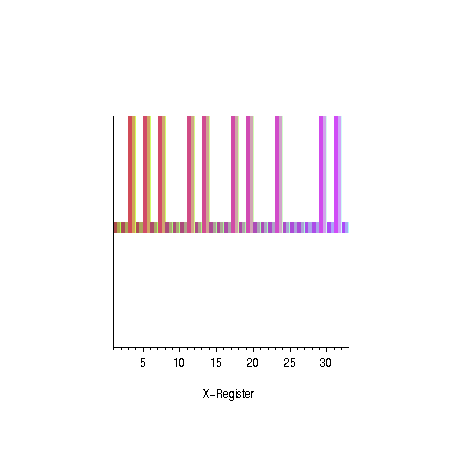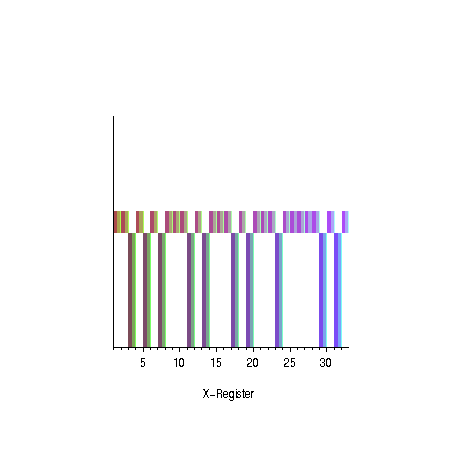 | 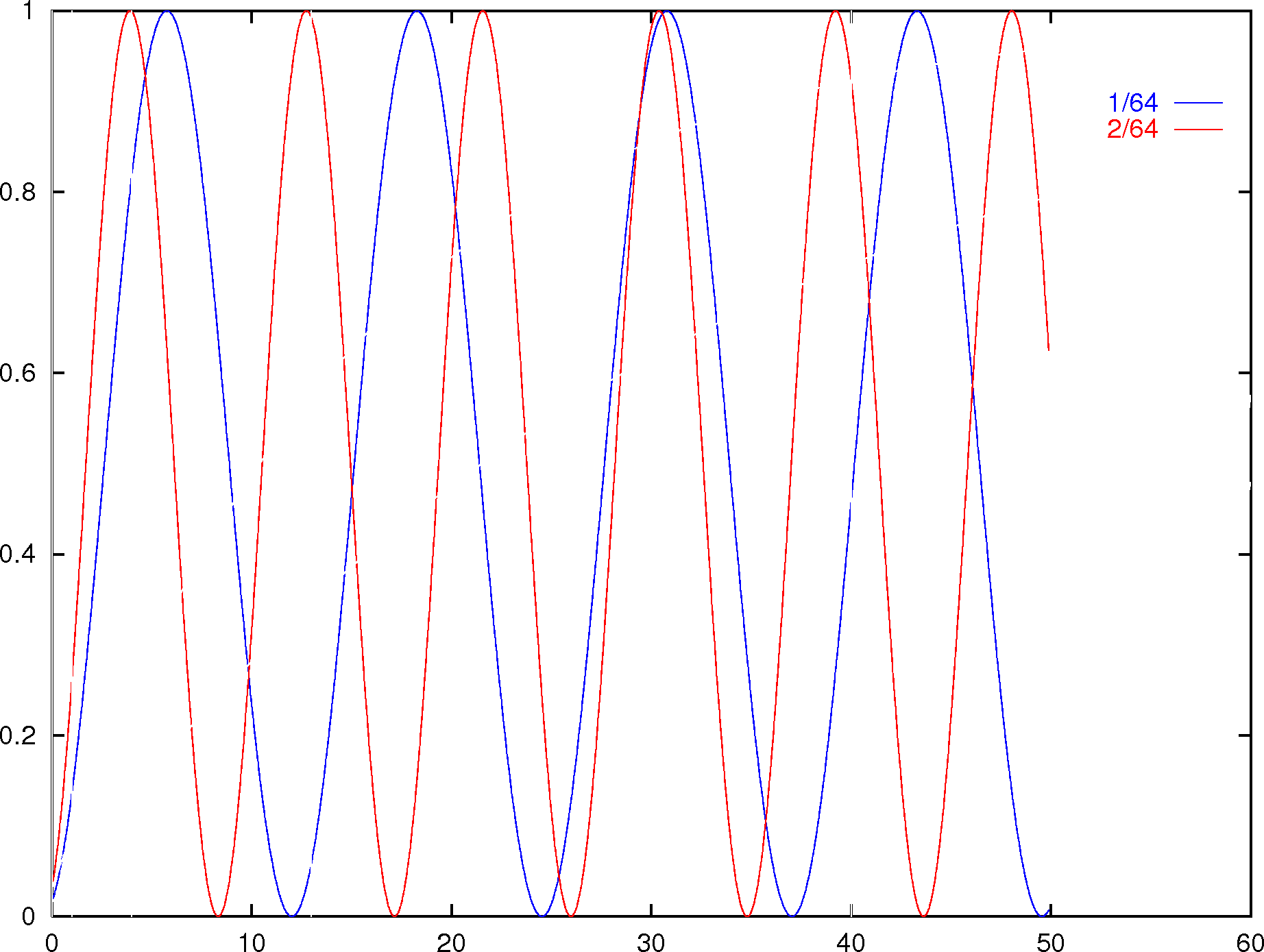 |
| oscillation of the amplitudes for the
odd prime numbers | succes probability as
a function of the number of iterations for different numbers
of solutions |
- reduction of the expected running time by ca. 12 % when
stopping before the maximum success probability is reached, see
Christof Zalka.
"Grover's quantum searching algorithm is optimal".
Physical Review A, vol. 60, no. 4, pp. 2746-2751, October 1999.
arXiv:quant-ph/9605034
- hybrid algorithm when the number t of solutions is unknown
- start with a small number of iterations
- increase the maximal number of iterations by the factor λ, 1<λ<4/3
- expected running time remains O(sqrt(N/t))
- for details see [M. Boyer, G. Brassard, P. Høyer and A. Tapp, 1998]
- exact quantum search
- instead of changing the sign of the states, multiply
them by a suitably chosen phase
- success probability 1 can be reached at
integral number of iterations
Peter Høyer.
"Arbitrary phases in quantum amplitude amplification."
Physical Review A, vol. 62, no, 5, 052304, October 2000.
DOI: 10.1103/PhysRevA.62.052304
arXiv:quant-ph/0006031
Lecture 15:
- amplitude amplification
- quantum algorithm without measurement corresponding to unitary tranformation V
- initial state |s⟩,
transformation I|s⟩=V(I - 2|s⟩⟨s|)V†
- target state |t⟩, characterised via Boolean function,
transformation I|t⟩=I - 2|t⟩⟨t|
- success probability p=|⟨t|V|s⟩|2
- iteration G'=-I|s⟩I|t⟩
- number of iterations O(sqrt(1/p))
Gilles Brassard, Peter Hoyer, Michele Mosca, and Alain Tapp.
"Quantum Amplitude Amplification and Estimation."
arXiv:quant-ph/0005055
- exact quantum algorithms
For a quantum algorithm with a priori known success
probability p, one can combine the techniques
of exact quantum search and amplitude
amplification to obtain a deterministic quantum algorithm.
- quantum counting
- use the conditional Grover iteration
|m⟩|x⟩ ↦ |m⟩Gm|x⟩
- Fourier transformation of the first register allows to
extract/approximate the period of G, from which
one can deduce the number of solutions
Gilles Brassard, Peter Hoyer, and Alain Tapp.
"Quantum counting."
in: Proceedings International Colloquium on Automata, Languages, and Programming
(ICALP 1998), pp. 820-831, 1998.
DOI: 10.1007/BFb0055105
arXiv:quant-ph/9805082
- analog quantum computing
- Hamiltonian simulation/quantum chemistry
- map the dynamics of a quantum system to e.g. a qubit system
- approximate the Hamiltonian by a sequence of "elementary" quantum transformations
- problem: complexity of the read-out, i.e., can the corresponding observable be efficiently
measured?
- solving linear systems
- goal: (approximate) solution of a linear
system A·x = b
- encode the vector b into a quantum state
|b⟩ = ∑i bi|i⟩
- solution is also encoded by a quantum state
|x⟩ = ∑i xi|i⟩
- problem: complexity of the read-out
Aram W. Harrow, Avinatan Hassidim, and Seth Lloyd.
"Quantum Algorithm for Linear Systems of Equations"
Physical Review Letter, vol. 103, no. 15, 150502 (2009).
DOI: 10.1103/PhysRevLett.103.150502
arXiv:1802.08227 [quant-ph]
Danial Dervovic, Mark Herbster, Peter Mountney, Simone
Severini, Nairi Usher, and Leonard Wossnig.
"Quantum linear systems algorithms: a primer."
arXiv:0811.3171 [quant-ph]
References
- Dagmar Bruß und Gerd Leuchs (Eds.)
Lectures on Quantum Information
Weinheim: Wiley-VCH, 2006.
ISBN 3-527-40527-5
- Matthias Homeister.
Quantum Computing verstehen
Heidelberg: Springer, 2013.
ISBN: 978-3-8348-1868-3
- Michael Nielsen und Isaac Chuang.
Quantum Computation and Information
Cambridge University Press, 2000.
ISBN: 978-0-5216-3503-5
DOI: 10.2277/0521635039
Weitere Informationen bei:

|
Markus Grassl
Max-Planck-Institut für die Physik des Lichts
Staudtstraße 2
91058 Erlangen
Telefon: +49 9131 7133 136
E-Mail: Markus.Grassl[at]mpl.mpg.de
|
Diese Seite wird betreut von
Markus Grassl
Letzte Änderung: 08.02.2019