- Bra-Ket-Schreibweise
- Zustandsraum
- Messung
- Zeitentwicklung eines geschlossenen Quantensystems (diskret/kontinuierlich)
- zusammengesetzte Quantensystme
- Quantenbit (qubit), Blochkugel
- Pauli-Matrizen
- Hadamard-Transformation
- fairer Münzwurf
- klassische (boolesche) Funktionen
- Ein-Qubit-Transformationen
- Quantengatter
- Quantenalgorithmus
- Initialisierung |00…0⟩
- Folge von elementaren unitären Transformationen
- Messung in Standardbasis
- die unitäre Transformation Uf : |x⟩|y⟩→|x⟩|y⊕f(x)⟩
- controlled NOT (CNOT)
- No-Cloning-Theorem
W. K. Wootters and W. H. Zurek.
"A single quantum cannot be cloned".
Nature, vol. 299, pp. 802-803 (1982).
DOI: 10.1038/299802a0
- verschränkte Zustände (entanglement)
- Messung von (|00⟩+|11⟩) in der Z-Basis
- Messung von (|00⟩+|11⟩) in der X-Basis
A. Einstein, B. Podolsky, and N. Rosen.
"Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?"
Physical Review, vol. 47, no. 10, pp. 777-780 (1935).
DOI: 10.1103/PhysRev.47.777 - Funktionsgraph einer klassischen Funktion f : {0,1}n→{0,1}m
- Messung des x-Registers
- Messung des y-Registers
- Bell-Basis
- Teleportation
Charles H. Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, and William K. Wootters.
"Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels".
Physical Review Letters, vol. 70, no. 13, pp. 1895-1899 (1993).
DOI: 10.1103/PhysRevLett.70.1895Gilles Brassard, Samuel L. Braunstein, Richard Cleve.
"Teleportation as a quantum computation".
Physica D, vol. 120, no. 1-2, pp. 43-47 (1998).
DOI: 10.1016/S0167-2789(98)00043-8
- Deutsch-Algorithmus
- entscheide, ob eine boolesche Funktion f : {0,1}→{0,1} konstant ist oder nicht
- klassisch: 2 Funktionsauswertungen
- Quantenalgorithmus: eine Anwendung von Uf
David Deutsch.
"Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer".
Proceedings of the Royal Society A, vol. 400, no. 1818, pp. 97-117, July 1985.
DOI: 10.1098/rspa.1985.0070 - Deutsch-Jozsa-Algorithmus
- gegeben: eine boolesche Funktion f : {0,1}n→{0,1}
- Ausgabe:
(A) f ist nicht konstant oder
(B) f ist nicht balanciert - klassisch: im schlimmsten Fall 2n-1+1 Funktionsauswertungen, im Mittel maximal 3 Auswertungen
- Quantenalgorithmus: eine Anwendung von Uf
- Analyse: Wahrscheinlichkeit, den Zustand |00…0⟩ zu messen
David Deutsch and Richard Jozsa.
"Rapid Solution of Problems by Quantum Computation".
Proceedings of the Royal Society A, vol. 493, no. 1907, pp. 553-558, December 1992.
DOI: 10.1098/rspa.1992.0167
- Algorithmus von Bernstein & Vazirani:
- gegeben: fa(x)=(-1)a⋅x
- bestimme: a∈{0,1}n
- Auswertung der klassischen Funktion fa liefert nur 1 Bit pro Auswertung
- Algorithmus von Simon
- gegeben fs : {0,1}n→{0,1}m (m≥n) mit fs(x)=fs(y) gdw. x=y oder x=y⊕s
- bestimme s∈{0,1}n
- Algorithmus
- Berechnung des Funktionsgraphen ∑x |x⟩|fs(x)⟩
- Hadamard-Transformation des ersten Registers
- Messung des ersten Registers liefert einen zufälligen Vektor z, der orthogonal ist zu s
- Wiederholung des Quantenalgorithmus, bis n-1 linear unabhängige Vektoren zi gefunden wurden
(hybrider Quantenalgorithmus: klassische while-Schleife mit Quanten-Unterprogramm) - nicht-triviale Lösung des homogenen linearen Gleichungssystems liefert einen Kandidaten s0
- teste, ob fs(s0)=fs(0)
D. R. Simon.
"On the power of quantum computation."
Proceedings 35th Annual Symposium on Foundations of Computer Science (FOCS 1994), pp. 116-123, November 1994.
DOI: 10.1109/SFCS.1994.365701
- Grundprinzip der RSA-Verschlüsselung
- Reduktion der Faktorisierung von N auf die Berechnung der Ordnung:
- bestimme die kleinste positive ganze Zahl r>0 mit ar≡1 mod N
- falls r gerade ist und ar/2≠-1 mod N, dann liefert ggt(ar/2±1,N) einen nicht-trivialen Faktor von N
- periodische Function f(x)=ax mod N
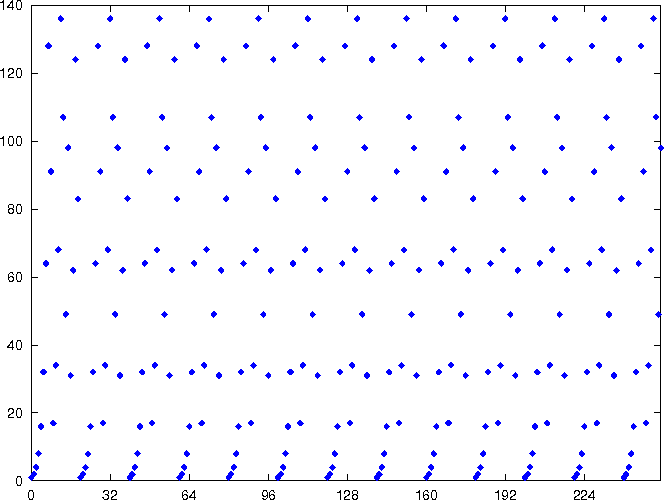
Funktionsgraph von 2x mod 165
- Fouriertransformation der Länge M=2×3×5×7×11×…
Peter W. Shor.
"Algorithms for quantum computation: discrete logarithms and factoring."
Proceedings 35th Annual Symposium on Foundations of Computer Science (FOCS 1994), pp. 124-134, November 1995.
DOI: 10.1109/SFCS.1994.365700 - Fouriertransformation der Länge M=2m
Peter W. Shor.
"Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer."
arXiv:quant-ph/9508027
- schnelle Quanten-Fourier-Transformation der Länge 2m
- Schlüsselaustausch nach Diffie-Hellman-Merkle
- diskreter Logarithmus dLog von c=gm:
- dLog über dem endlichen Körper Z/pZ, aber auch andere endliche Köper, elliptische Kurven
- Funktion f(x,y)=cxg-y=(gm)xg-y=gmx-y
- Urbilder sind Geraden der Steigung m
- zweidimensionale Fourier-Transformation eliminiert die Verschiebung
Post Quantum Cryptography
- Motivation
- Viele kryptographische Verfahren, wie beispielsweise die RSA-Verschlüsselung, werden unsicher, wenn es Quantencomputer gibt.
- Langzeitsicherheit: neue Verfahren, die (hoffentlich) auch sicher sind, wenn es Quantencomputer gibt.
- speziell: Public-key-Verfahren
- Codierungsbasierte Kryptographie
- fehlerkorrigierender Code:
- lineare Abbildung in einen höherdimensionalen Vektorraum über einem endlichen Körper
- Fehler an einer begrenzten Anzahl von Positionen können korrigiert werden
- McEliece-Verfahren
- Verschlüsselung durch permutierte lineare Abbildung und Addition von zufälligen Fehlern (Rauschen)
- Entschlüsselung durch effizienten Decodierungsalgorithmus (Fehler können korrigiert werden)
- allgemeines Decodierproblem ist NP-hart; aber unklar, ob die spezielle Variante immer noch NP-hart ist
Robert J. McEliece.
"A Public-Key Cryptosystem Based on Algebraic Coding Theory"
Jet Propulsion Labs Deep Space Network Progress Report, 42-44, pp. 114-116, 1978.
- fehlerkorrigierender Code:
- Gitterbasierte Kryptographie
- Gitter: Punktmengen, definiert über alle ganzzahligen Summen von Basisvektoren (die Basis ist nicht eindeutig)
- schwere Probleme (Shortest Vector Problem, Closest Vector Problem, Shortest Independent Vectors Problem)
- Verfahren von Goldwasser, Goldreich & Halevi (1997)
- Verschlüsselung in "schlechter Basis" (bekannt über Hermite Normal Form), Addition von "Rauschen"
- Entschlüsselung in "guter Basis" (Basisvektoren möglichst orthogonal) effizient möglich
Oded Goldreich, Shafi Goldwasser and Shai Halevi.
"Public-key cryptosystems from lattice reduction problems".
in Advances in Cryptology - CRYPTO '97, Lecture Notes in Computer Science, vol. 1294, pp 112-131, 1997.
DOI: 10.1007/BFb0052231
- weiterführende Literatur
Daniel J. Bernstein, Johannes Buchmann and Erik Dahmen (Eds.).
Post-Quantum Cryptography.
Springer, Berlin. 2009.
DOI: 10.1007/978-3-540-88702-7
- One Time Pad Protocol
- Information theoretically secure when an authenticated public classical channel is used.
- Channel authentication crucial. Possibility of Man-in-the-Middle attack otherwise.
- Quantum Key Distribution: (QKD): The BB84 protocol
Charles H. Bennett and Gilles Brassard.
"Quantum cryptography: Public key distribution and coin tossing".
In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, 1984.
http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf- The no-cloning theorem, complementarity of non-commuting observables.
- Preparation of non-orthogonal states and measurement with non-commuting observables.
- Post processing: sifting, parameter estimation, information reconciliation and privacy amplification.
- Security analysis against intercept-resend attacks.
- Different types of attacks on QKD: individual (e.g., intercept-resend), collective, and coherent attacks.
- Practical issues: non ideal single photon sources and detectors, photon-number-splitting attack, decoy state protocol.
- Brief introduction to Continuous Variable (CV) QKD
- The quantum harmonic oscillator, quadrature operators, Heisenberg uncertainty relation.
- An outline of QKD based on Gaussian modulated coherent states: the GG02 protocol.
Frédéric Grosshans and Philippe Grangier.
"Continuous Variable Quantum Cryptography Using Coherent States".
Physical Review Letters, vol. 88, no. 5, 057902 (2002).
DOI: 10.1103/PhysRevLett.88.057902 - Further Reading:
- suche eines Urbilds x einer booleschen Funktion f : {0,1}n→{0,1} mit f(x)=1
- Erfüllbarkeitsproblem für boolesche Formeln (3-SAT, NP-vollständig)
- keine Suche im Telefonbuch bzw. in einer Datenbank
Lov K. Grover.
"A fast quantum mechanical algorithm for database search."
arXiv:quant-ph/9605043 - Reduktion auf zweidimensionale Dynamik (Zustände mit f(x)=1 bzw. f(x)=0)
- geometrische Interpretation als Kombination von zwei Spiegelungen,
siehe Kapitel 6.3 inMatthias Homeister.
Quantum Computing verstehen.
Heidelberg: Springer, 2013.
ISBN: 978-3-8348-1868-3 - exakte Lösung der Rekursionsgleichung für die Amplituden
Michel Boyer, Gilles Brassard, Peter Høyer and Alain Tapp.
"Tight bounds on quantum searching."
Fortschritte der Physik, vol. 46, no. 4-5, pp. 493-505, June 1998.
DOI: 10.1002/(SICI)1521-3978(199806)46:4/5<493::AID-PROP493>3.0.CO;2-P
arXiv:quant-ph/9605034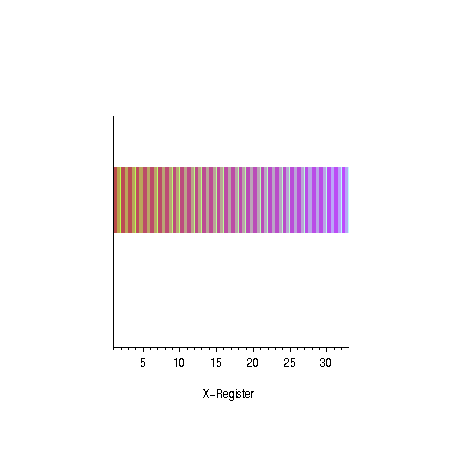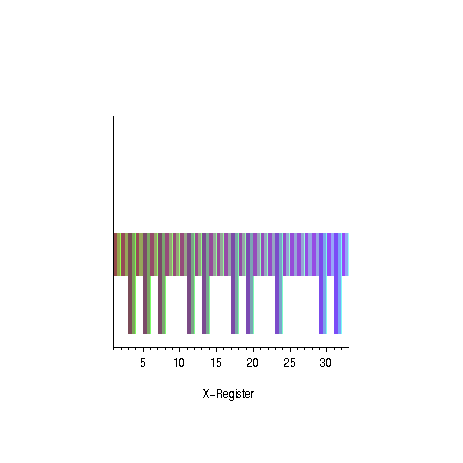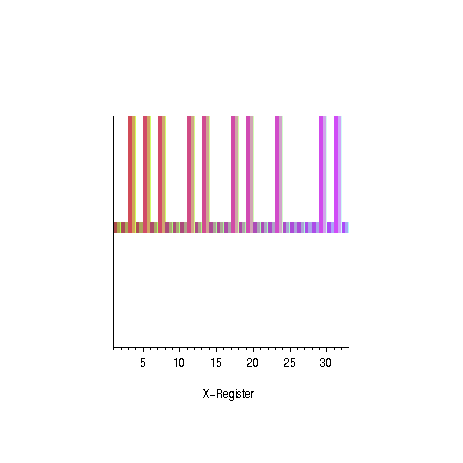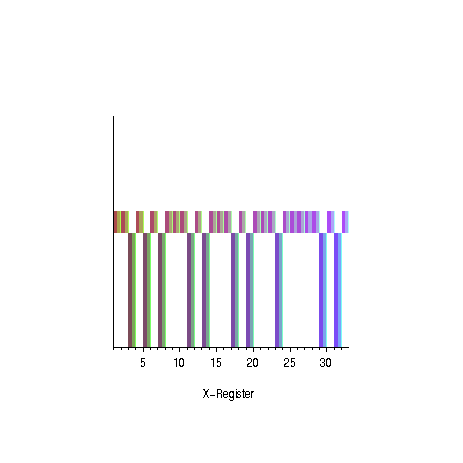
> 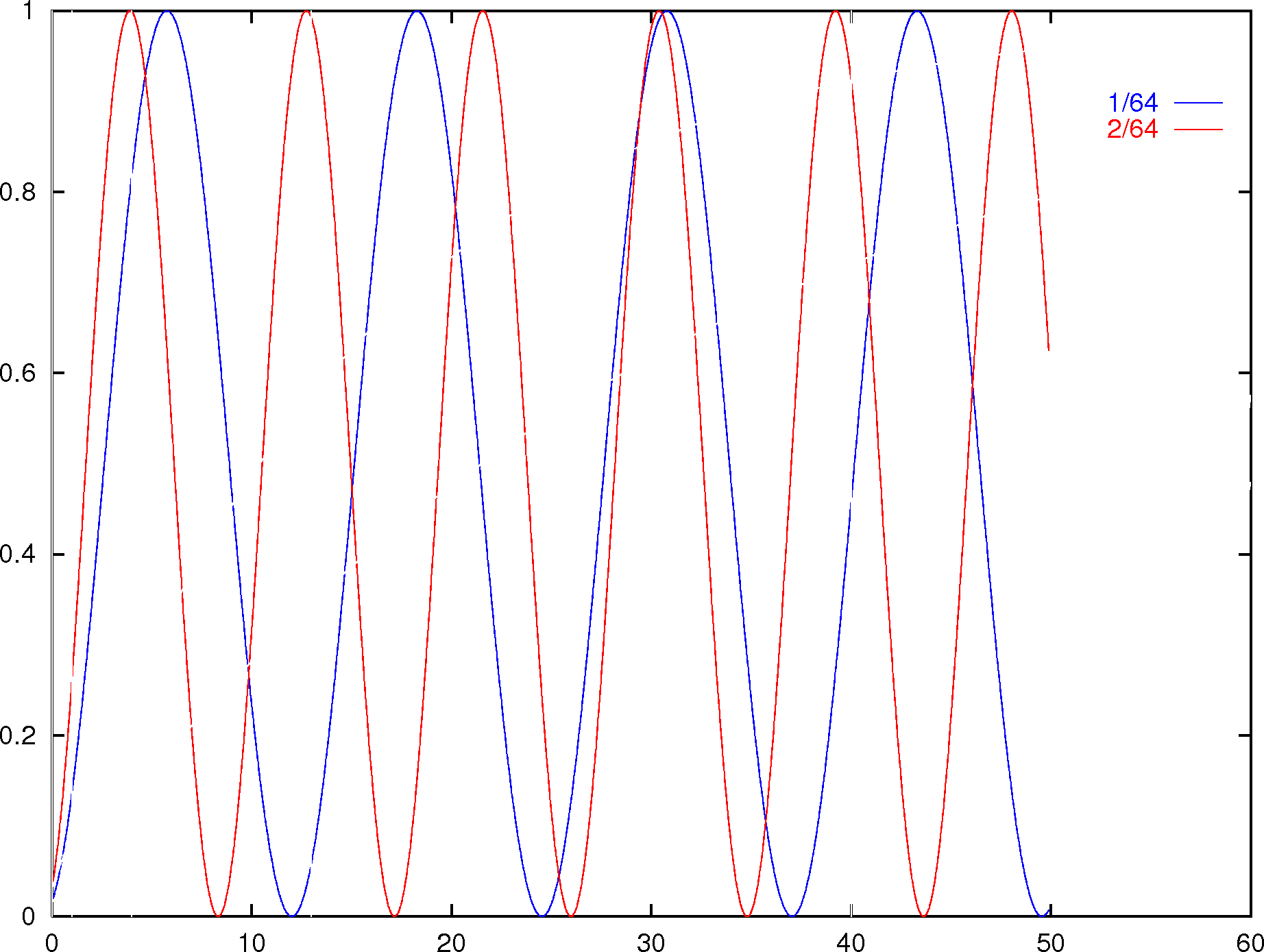
Oszillation der Amplituden für ungerade Primzahlen Erfolgswahrscheinlichkeit in Abhängigkeit der Anzahl der Lösungen - Reduktion der erwarteten Laufzeit um ca. 12 % möglich, siehe
Christof Zalka.
"Grover's quantum searching algorithm is optimal".
Physical Review A, vol. 60, no. 4, pp. 2746-2751, October 1999. arXiv:quant-ph/9605034
- Speziallfall t/N=4: nur eine Iteration liefert mit Sicherheit eine Lösung
- hybrider Algorithmus bei unbekannter Anzahl t der Lösungen
- starte mit einer kleine Anzahl Iterationen
- vergrößere die maximale Anzahl der Iterationen um den Faktor λ, 1<λ<4/3
- erwartete Laufzeit weiterhin O(sqrt(N/t))
- siehe [M. Boyer, G. Brassard, P. Høyer and A. Tapp, 1998]
- amplitude amplification
- Quantenalgorithmus ohne Messung als unitäre Transformation U
- Anfangszustand |s⟩, Transformation I|s⟩=U(I - 2|s⟩⟨s|)U†
- Zielzustand |t⟩ durch boolesche Funktion charakterisiert, Transformation I|t⟩=I - 2|t⟩⟨t|
- Erfolgswahrscheinlichkeit p=|⟨t|U|s⟩|2
- Iteration G'=-I|s⟩I|t⟩
- Anzahl Iterationen O(sqrt(1/p))
Gilles Brassard, Peter Hoyer, Michele Mosca, and Alain Tapp.
"Quantum Amplitude Amplification and Estimation."
arXiv:quant-ph/0005055 - deterministischer Algorithmus bei bekannter Anzahl Lösungen/bekannter Erfolgswahrscheinlichkeit
- Modifikation des Algorithmus, so dass das Maximum der Oszillation bei einer ganzen Zahl von Iterationen liegt
- deterministischer Algorithmus für das Problem von Simon
- in jedem Teilschritt sucht man einen zu s orthogonalen Vektor z, der linear unabhängig ist von den bisherigen Vektoren
- Anzahl der Vektoren bekannt (falls s≠0)
- Konbination mit deterministischem Suchalgorithmus
Gilles Brassard and Peter Hoyer.
"An Exact Quantum Polynomial-Time Algorithm for Simon's Problem."
arXiv:quant-ph/9704027
