- Bra-Ket-Schreibweise
- Zustandsraum
- Messung
- fairer Münzwurf
- Zeitentwicklung eines geschlossenen Quantensystems (diskret/kontinuierlich)
- zusammengesetzte Quantensysteme
- Tensorprodukt von Vektorräumen, Vektor, Matrizen
- Dynanik ohne Wechselwerkung
- Messung eines Teilsystem
- Verschränkung (Entanglement)
Beispiel |Ψ+⟩=1/sqrt(2)(|00⟩+|11⟩)
- Quanten-Bit (Qubit)
- Bloch-Kugel
- Quanten-Register mit n Qubits
- Standard-Basis B={|x1,x2,…xn⟩: xi ∈ {0,1}n }
- reversible klassische Funktionen:
f: {0,1}n → {0,1}m- ergänze die Funktion f um zusätzliche Ausgaben. so dass sie injektiv ist
- allgemein: f~: (x,y) → (x,y⊕f(x))
- spezielle Funktionen:
- NOT: x → 1-x
- CNOT: (x,y) → (x,x⊕y)
- Toffoli: (x,y,z) → (x,y,x⋅y⊕z)
- die unitäre Transformation Uf : |x⟩|y⟩→|x⟩|y⊕f(x)⟩
- No-Cloning-Theorem
W. K. Wootters and W. H. Zurek.
"A single quantum cannot be cloned".
Nature, vol. 299, pp. 802-803 (1982).
DOI: 10.1038/299802a0
- Funktionsgraph einer klassischen Funktion f : {0,1}n→{0,1}m
- Messung des x-Registers
- Messung des y-Registers
- Relationen zwischen CNOT, den Pauli-Matrizen und der Hadamard-Matrix
- diagonale Version einer booleschen Funktion: |x⟩ → (-1)f(x)|x⟩
- Deutsch-Algorithmus
- entscheide, ob eine boolesche Funktion f : {0,1}→{0,1} konstant ist oder nicht
- klassisch: 2 Funktionsauswertungen
- Quantenalgorithmus: eine Anwendung von Uf
David Deutsch.
"Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer".
Proceedings of the Royal Society A, vol. 400, no. 1818, pp. 97-117, July 1985.
DOI: 10.1098/rspa.1985.0070
JSTOR: www.jstor.org/stable/2397601
- detaillierte Analyse des Deutsch-Algorithmus
- Deutsch-Joza-Algorithmus
- gegeben: eine boolesche Funktion f : {0,1}n→{0,1}
- Ausgabe:
(A) f ist nicht konstant oder
(B) f ist nicht balanciert - klassisch: im schlimmsten Fall 2n-1+1 Funktionsauswertungen,
im Mittel maximal 3 Auswertungen (siehe Table 1 im Originalartikel) - Quantenalgorithmus: eine Anwendung von Uf
David Deutsch und Richard Jozsa.
"Rapid Solution of Problems by Quantum Computation".
Proceedings of the Royal Society A, vol. 493, no. 1907, pp. 553-558, Dezember 1992.
DOI: 10.1098/rspa.1992.0167
JSTOR: www.jstor.org/stable/52182
- Deutsch-Joza-Algorithmus (Fortsetzung)
- Wahrscheinlichkeit, das Ergebnis 00…0 zu messen
- äquivalente Fragestellung: Wahrscheinlichkeit der Projektion des Zustands vor der Hadamard-Transformation auf den Zustand H⊗n|0⟩
- Vergleich: klassische Funktion f, quantenmechanische Variante Uf
- Das Problem von Simon
- klassische Funktion fs:
{0,1}n
→{0,1}m (m≥n),
zusätzlich: fs(x)=fs(y) genau dann, wenn x=y oder x=y⊕s für einen festen Vektor s∈{0,1}n - gesucht ist der Vektor s
- klassisch: im schlimmsten Fall 2n-1+1 Auswertungen von fs, um eine Kollision zu finden
Erwartungswert O(2n/2) AuswertungenD. R. Simon.
"On the power of quantum computation."
Proceedings 35th Annual Symposium on Foundations of Computer Science (FOCS 1994), pp. 116-123, November 1994.
DOI: 10.1109/SFCS.1994.365701
- klassische Funktion fs:
{0,1}n
→{0,1}m (m≥n),
- Simons Algorithmus (Fortsetzung)
- Präparation des Funktionsgraphen ∑x|x⟩|fs(x)⟩
- Messung des zweiten Registers
- Superposition der zugehörigen Urbilder
- Hadamard-Transformation
- Messung des ersten Registers liefert Vektor y mit y⋅s=0
- Wiederholung, bis n-1 linear unabhängige Vektoren y gefunden wurden
- nicht triviale Lösung s' des linearen Gleichungssystems
- abschließender Test, ob fs(0)=fs(s')
- erwartete Anszahl der Wiederholungen O(n)
- reiner Quantenalgorithmus
- Präperation eines festen Ausgangszustands
- Folge von unitären Transformationen auf einer beschränkten Anzahl von Qubits
beliebige Ein-Qubit-Operationen und CNOT genügen, um beliebige unitäre Operationen zu implementierenAdriano Barenco, Charles H. Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, and Harald Weinfurter.
"Elementary gates for quantum computation."
Physical Review A, vol. 52, no. 5, pp. 3457-3467, 1995.
DOI: 10.1103/PhysRevA.52.3457
- hybrider Quantenalgorithmus
- reine Quantenalgorithmen mit fester Laufzeit als Unterprogramme
- klassischen Schleifen (while/repeat)
- Faktorisiserungsalgorithmus von Shor
- finde nicht-triviale Faktoren einer ganzen Zahl N
- einfach, falls N gerade ist
- allgemein: Laufzeit des besten bekannten klassischen Verfahrens (allgemeines) Zahlkörpersieb
O(exp[(C+o(1))(log N)1/3(log log N)2/3]) mit C=(64/9)1/3≈1.923 - Reduktion auf Ordnungsbestimmung:
- bestimme die kleinste positive ganze Zahl r>0 mit ar ≡ 1 mod N
- falls r gerade ist und ar/2≠-1 mod N, dann liefert ggT(ar/2±1,N) einen nicht-trivialen Faktor von N
- periodische Function f(x)=ax mod N
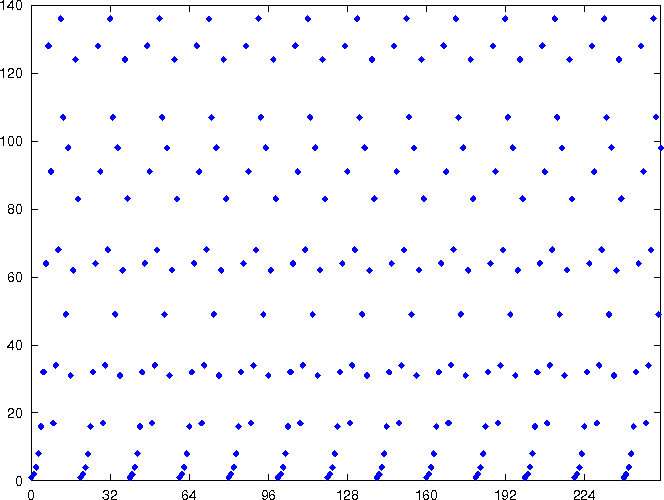
Funktionsgraph von 2x mod 165 - Fouriertransformation der Länge M=2×3×5×7×11×…
Peter W. Shor.
"Algorithms for quantum computation: discrete logarithms and factoring."
Proceedings 35th Annual Symposium on Foundations of Computer Science (FOCS 1994), pp. 124-134, November 1995.
DOI: 10.1109/SFCS.1994.365700 - Fouriertransformation der Länge M=2m
Peter W. Shor.
"Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer."
arXiv:quant-ph/9508027
(Ulrich Seyfarth)
- klassische Verschlüsselungsverfahren
- symmetrische Verfahren (gemeinsamer geheimer Schlüssel)
- asymmetrische Verfahren (privater und öffentlicher
Schlüssel)
Empfänger verteilt öffentliche Schlüssel und lässt sich geheime Nachrichten schicken, vgl. PGP - one-time Pad (zufälliger Schlüssel, gleich lang wie Nachricht, nur einmal verwendbar, informationstheoretisch sicher, Problem: Schlüsselaustausch)
- Verschlüsselungsverfahren nach Rivest, Shamir, Adleman (RSA)
- öffentlicher Schlüssel: modulus N, Exponent e
- privater Schlüssel:
- Faktorisierung N = pq
- inverser Exponent e, d. h., de = 1 mod φ(N), ggT(e,φ(N) = de + sφ(N)
- Eulersche Phi-Funktion (Euler's totient function):
φ(N) ist die Anzahl der zu N teilerfremden positiven ganzen Zahlen, die echt kleiner sind als N sind - weil p und q prim und teilerfremd sind, gilt φ(N)=(p-1)(q-1)
- Verschlüsselung: m → me mod N
- Entschlüsselung: me → (me)d = m mod N
- Angriff auf den privaten Schlüssel:
Faktorisierung von N = pq erlaubt Berechnung von φ(N) und d = e-1 mod φ(N) - Angriff auf die Nachricht:
e-te Wurzel aus me bzw. aus me + kN, wobei die ganze Zahl k unbekannt ist
- Schlüsselaustausch nach Diffie-Hellman-Merkle
- öffentlich bekannt: Primzahl p und Basis g
- Alice und Bob wählen individuelle private Exponenten a bzw. b
- Alice sendet ga mod p an Bob; und Bob sendet ga mod p an Alice
- der gemeinsame Schlüssel ist (ga)b mod p = (gb)a mod p
- Sicherheit beruht auf Schwierigkeit der Berechnung des diskreten Logarithmus dlogg (ga) = a
- Quantenschlüsselaustausch nach Bennett und Brassard (BB84)
- Generierung eines gemeinsamen geheimen Schlüssels, z. B. für one time pad
- Sicherheit beruht auf Grundlagen der Quantentheorie
- Alice und Bob verbindet ein Quantenkanal und ein authentisierter klassischer Kanal
- Alice erzeugt zufällige Bits 0 oder 1, codiert sie in einer zufälligen Basis Z oder X und schickt die Quantenzustände über den Quantenkanal zu Bob
- Bob misst zufällig in der Basis Z oder X
- nach der Messung sendet Bob die Information, in welcher Basis welches Qubit gemessen wurde, über den authentischen klassischen Kanal an Alice
- Alice teilt Bob mit, wann die Basen übereinstimmen
- ein Teil der klassischen Bits wird verglichen zur Fehlerabschätzung
- Lauscher erzeugt Fehler (no cloning), bei einfachstem Angriff (intercept-resend) messen Alice und Bob 25% Fehlerrate, falls ein Lauscher jedes Bit zufällig in Z bzw. X misst und neu weiterschickt
- Fehler können durch Austausch durch Prüfbits
über den klassischen Kanal korrigiert werden;
Angreifer erhalten Teilinformation über die geheimen Bits;
die mögliche Information des Lauschers kan durch privacy amplification verringert werden;
die Fehlerrate darf nicht zu hoch sein - Realisierung des Quantenkanals beispielsweise durch polarisierte Photonen
Charles H. Bennett and Gilles Brassard.
"Quantum cryptography: Public key distribution and coin tossing".
In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, 1984.
http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf
- Berechnung des diskreten Logarithmus (P. Shor)
- gegeben: Basis g und modulus p
(Primzahl),
gesucht: ganze Zahl a mit c=ga mod p - Ansatz Funktion f(x,y)=cx g-y=gax-y mod p
- Funktionsgraph: |ψ⟩=1/(p-1) ∑x∑ y|x⟩|y⟩|cx g-y mod p⟩
- nach Messung des dritten Registers entspricht der Zustand der ersten beiden Register einer Geraden y=ax+y0 mit Steigung a und zufälliger Verschiebung y0
- zweidimensionale diskrete Fouriertransformation DFT(p-1)×(p-1)=DFT(p-1)⊗DFT(p-1) transformiert die Verschiebung in eine Phase und ergibt eine Ursprungsgerade mit inverser Steigung
- Messung der ersten beiden Register erlaubt die Brechnung von a, falls nicht der Punkt (0,0) gemessen wird
- gegeben: Basis g und modulus p
(Primzahl),
- Verallgemeinerung: Exponentialfunktion/diskreter Logarithmus für endliche Gruppen
- verborgene Untergruppen (Hidden Subgroup Problem)
- gegeben: eine (endliche) Gruppe G und eine Funktion f, die konstant ist auf Nebenklassen einer unbekannten Untergruppe H≤G, d. h., f(x)=f(y) gdw. x y-1 ∈ H
- gesucht: Erzeuger für H
- effiziente Quantenalgorithmen für alle (endlichen)
abelschen Gruppen und manche nicht-abelsche Gruppen
- Simon's Problem: G = (Z2)n, H={0,s}
- Faktorisierung: G = Zφ(N), H = ⟨a⟩
- diskreter Logarithmus: G = Zp-1 × Zp-1, H = ⟨(1,a)⟩
- suche eines Urbilds x einer booleschen Funktion f : {0,1}n→{0,1} mit f(x)=1
- Erfüllbarkeitsproblem für boolesche Formeln (3-SAT, NP-vollständig)
- keine Suche im Telefonbuch bzw. in einer Datenbank
Lov K. Grover.
"A fast quantum mechanical algorithm for database search."
arXiv:quant-ph/9605043 - Reduktion auf zweidimensionale Dynamik (Zustände mit f(x)=1 bzw. f(x)=0)
- geometrische Interpretation als Kombination von zwei Spiegelungen,
siehe Kapitel 6.3 inMatthias Homeister.
Quantum Computing verstehen.
Heidelberg: Springer, 2013.
ISBN: 978-3-8348-1868-3 - exakte Lösung der Rekursionsgleichung für die Amplituden
Michel Boyer, Gilles Brassard, Peter Høyer and Alain Tapp.
"Tight bounds on quantum searching."
Fortschritte der Physik, vol. 46, no. 4-5, pp. 493-505, June 1998.
DOI: 10.1002/(SICI)1521-3978(199806)46:4/5<493::AID-PROP493>3.0.CO;2-P
arXiv:quant-ph/9605034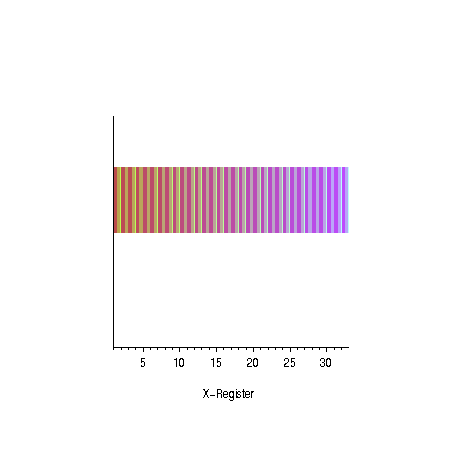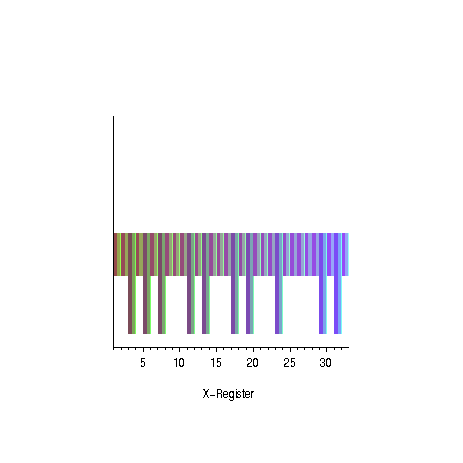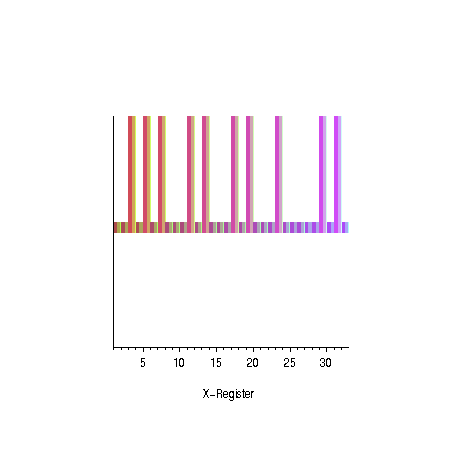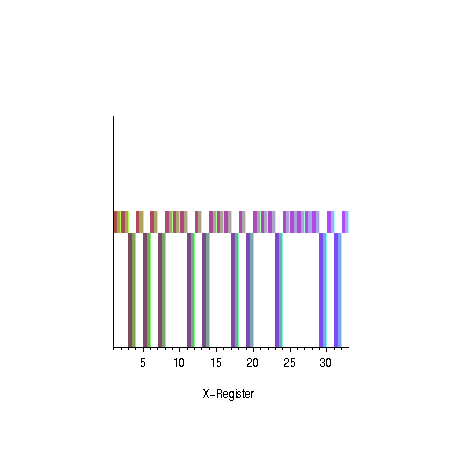
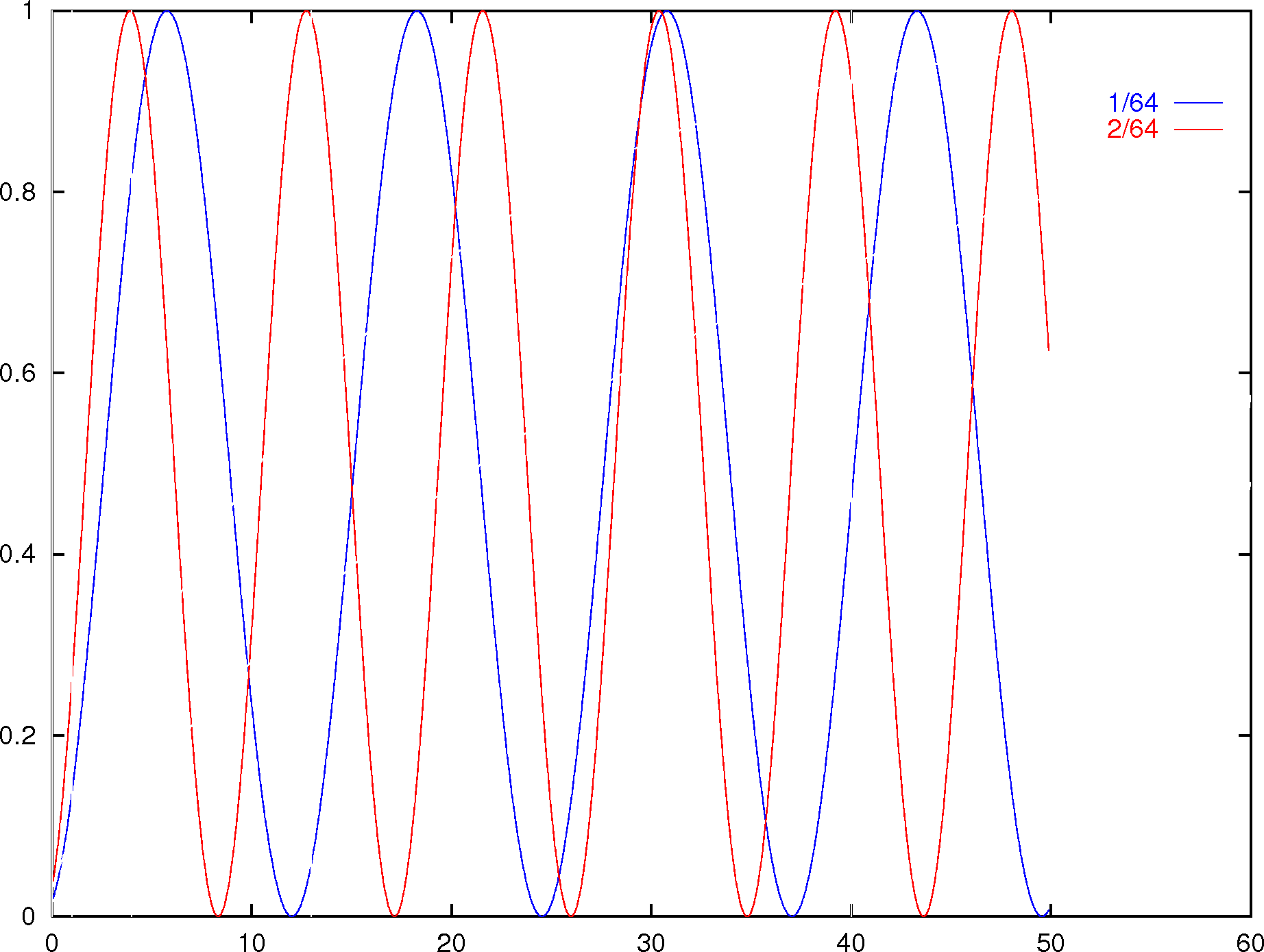
Oszillation der Amplituden für ungerade Primzahlen Erfolgswahrscheinlichkeit in Abhängigkeit der Anzahl der Lösungen
- Reduktion der erwarteten Laufzeit um ca. 12 % möglich, siehe
Christof Zalka.
"Grover's quantum searching algorithm is optimal".
Physical Review A, vol. 60, no. 4, pp. 2746-2751, October 1999. arXiv:quant-ph/9605034 - hybrider Algorithmus bei unbekannter Anzahl t der Lösungen
- starte mit einer kleine Anzahl Iterationen
- vergrößere die maximale Anzahl der Iterationen um den Faktor λ, 1<λ<4/3
- erwartete Laufzeit weiterhin O(sqrt(N/t))
- siehe [M. Boyer, G. Brassard, P. Høyer and A. Tapp, 1998]
- amplitude amplification
- Quantenalgorithmus ohne Messung als unitäre Transformation U
- Anfangszustand |s⟩, Transformation I|s⟩=U(I - 2|s⟩⟨s|)U†
- Zielzustand |t⟩ durch boolesche Funktion charakterisiert, Transformation I|t⟩=I - 2|t⟩⟨t|
- Erfolgswahrscheinlichkeit p=|⟨t|U|s⟩|2
- Iteration G'=-I|s⟩I|t⟩
- Anzahl Iterationen O(sqrt(1/p))
Gilles Brassard, Peter Hoyer, Michele Mosca, and Alain Tapp.
"Quantum Amplitude Amplification and Estimation."
arXiv:quant-ph/0005055
- Erfolgswahrscheinlichkeit a priori bekannt
- verallgemeinerte Spiegelungen der Form IΦ|t⟩=I - (1-eiΦ)|t⟩⟨t|
- Wahl der Phase Φ, so dass die maximale Erfolgswahrscheinlichkeit bei einer ganzzahligen Anzahl von Iterationen erreicht wird
